题目描述

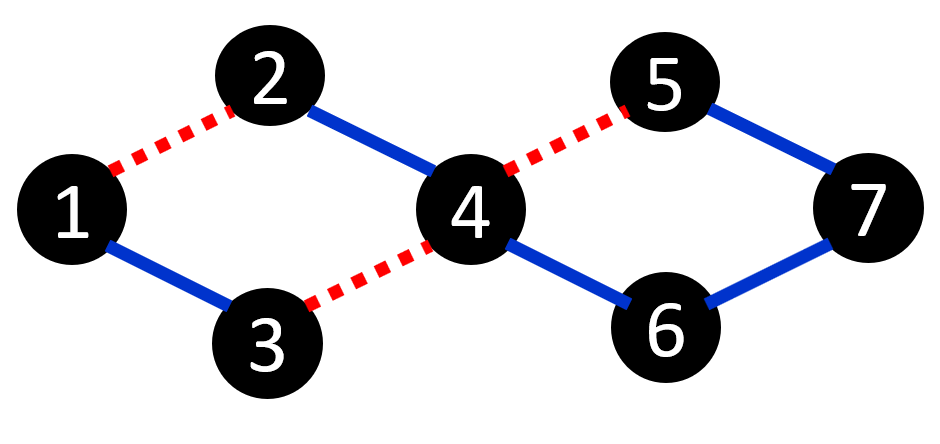
Alice colors each edge in the graph red or blue.

A path is a sequence of edges where each pair of consecutive edges have a node in common. If the first edge in the pair is of a different color than the second edge, then that is a ``color change.''

After Alice colors the graph, Bob chooses a path that begins at node $1$ and ends at node $N$. He can choose any path on the graph, but he wants to minimize the number of color changes in the path. Alice wants to choose an edge coloring to maximize the number of color changes Bob must make. What is the maximum number of color changes she can force Bob to make, regardless of which path he chooses?

输入格式

The first line contains two integer values $N$ and $M$ with $2 \le N \le 100\,000$ and $1 \le M \le 100\,000$. The next $M$ lines contain two integers $a_i$ and $b_i$ indicating an undirected edge between nodes $a_i$ and $b_i$ ($1 \le a_i, b_i \le N$, $a_i \not= b_i$).

All edges in the graph are unique.

输出格式

Output the maximum number of color changes Alice can force Bob to make on his route from node $1$ to node $N$.

样例

输入样例1

3 3
1 3
1 2
2 3

输出样例1

0

输入样例2

7 8
1 2
1 3
2 4
3 4
4 5
4 6
5 7
6 7

输出样例2

3